Let's Learn Algorithms: An Introduction to Bubble Sort

This is the first post in the Let's Learn Algorithms series, so if you are unfamiliar with what to expect I suggest you click the link and get a basic understanding of how this series works.

If you want to watch this in a video with examples using cards you can watch the video below. Otherwise continue on and read the article. The same content is covered in both places.

Now, without wasting any time, let’s jump right into learning about our first algorithm, bubble sort!

What is bubble sort?

Bubble sort is a sorting algorithm (duh!), which essentially means that it is an algorithm used to take an unordered list and to put them into a certain order.

For learning purposes, this typically means taking a list of numbers and sorting them in non-decreasing order. For example, you could take the list 5, 4, 2, 3, 1, 0 and after sorting it you would get 0, 1, 2, 3, 4, 5.

That said, not all sorting deals with numbers, and it most definitely doesn’t always consist of numbers in increasing order. These are mostly just used for teaching, and then in the practice problems I will include a few problems that DO NOT involve sorting numbers in increasing order.

Bubble sort isn’t the most efficient sorting algorithm, but it does have two primary benefits over many other sorting algorithms.

First, it is one of the simplest sorting algorithms to implement, especially for a beginner, so it serves as a very handy learning tool and as a simple way to sort relatively small lists.

Second, we can easily detect when a list is already sorted with bubble sort and terminate our code early, making it useful when we are provided with a sorted list but do not know ahead of time that the list is sorted.

How does it work?

Bubble sort works by walking through a list of numbers and comparing each consecutive pair of numbers. When we compare the numbers we will ask “is the first number greater than the second number?” and if the answer is yes, we swap the position of each number in the pair.

Regardless of whether or not we swap the numbers, we then move on to the next consecutive pair in the list and repeat the comparison and potential swap steps.

Walking through an example of comparing and swapping items

This is much clearer with an example, so lets go back to the original example of 5, 4, 2, 3, 1, 0.

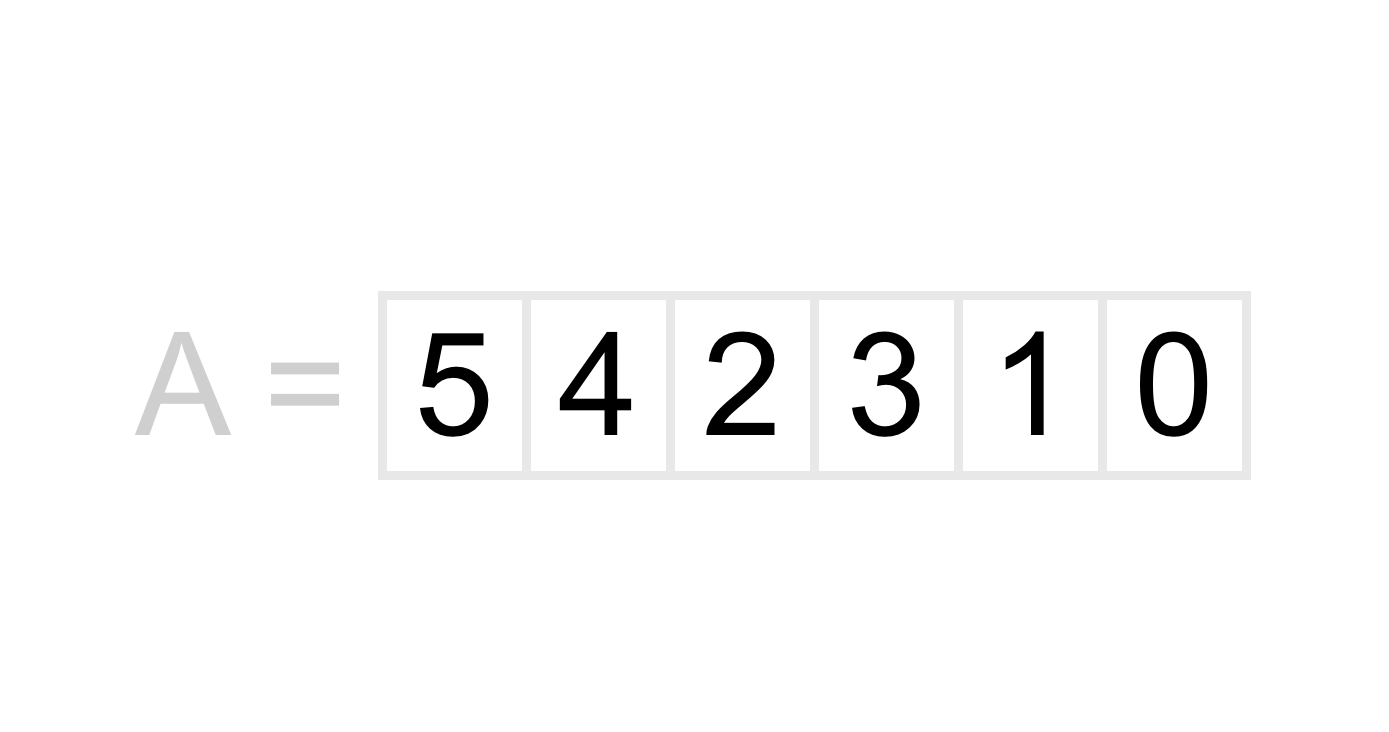
The first pair we would look at is the pair 5 and 4. 5 is the “first” number in our pair, and 4 is the second number in our pair.

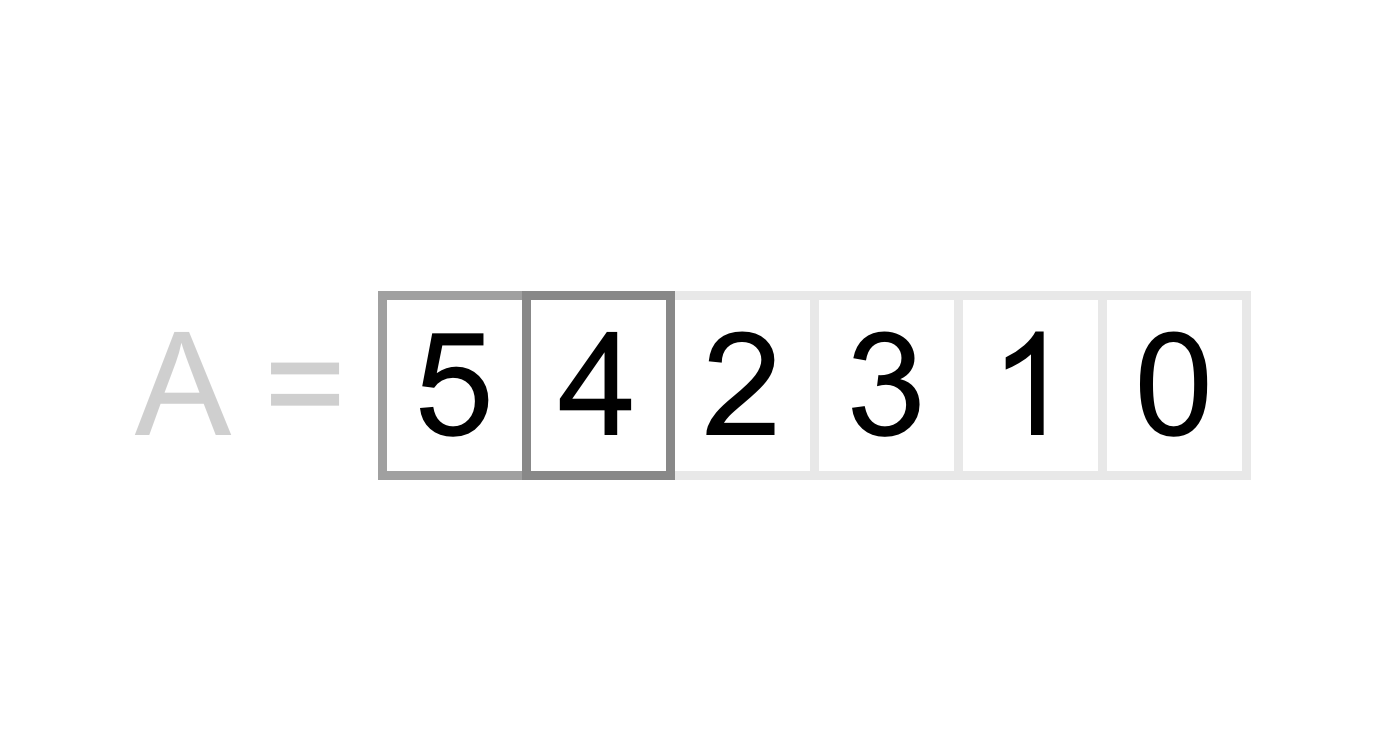
We want to sort our numbers in non-decreasing order, so we first ask “is 5 greater than 4?”. The answer we get to this question is yes! 5 is greater than 4, so we need to swap the positions of 4 and 5.

After swapping these two numbers we get the following list of numbers as a result.

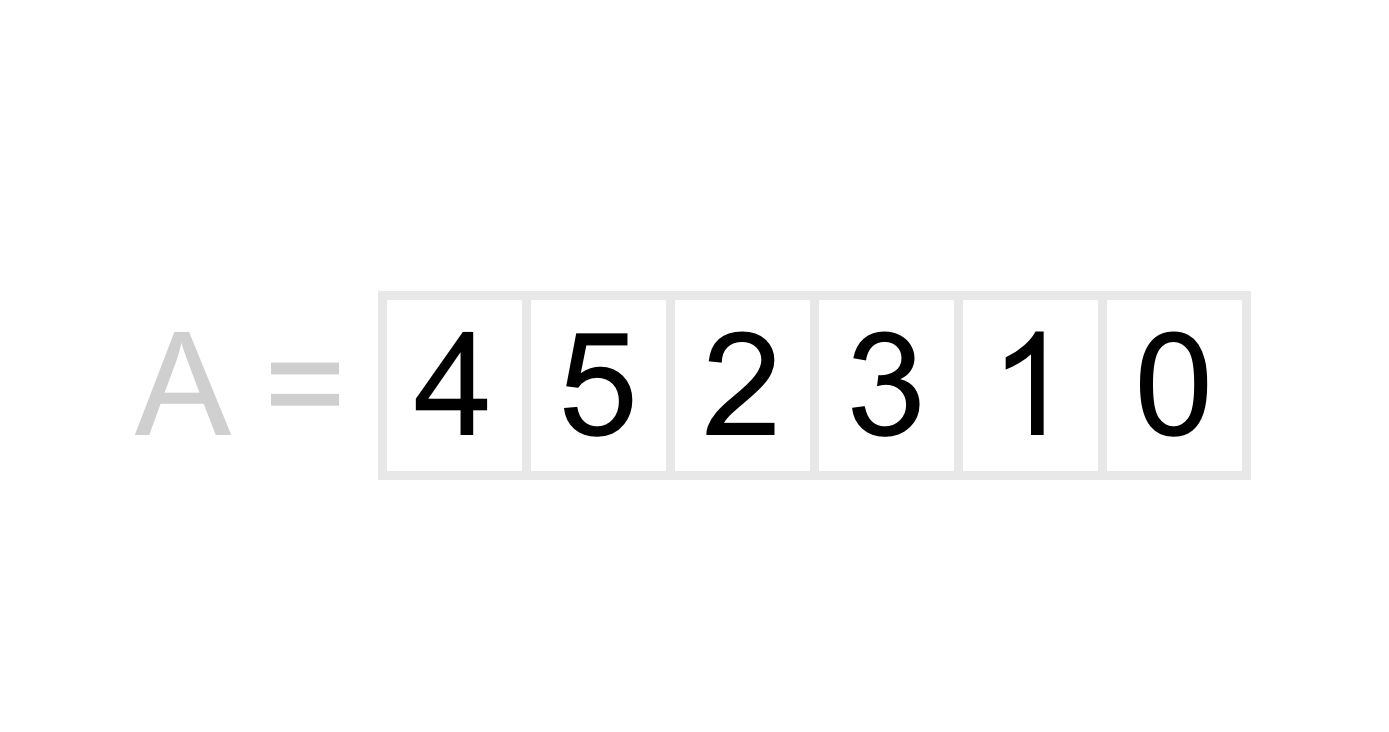
Next we need to move on to the next pair in the list. When we move on to the next pair we only move over by one position, not two! That means that the next pair we will be looking at is 5 and 2.

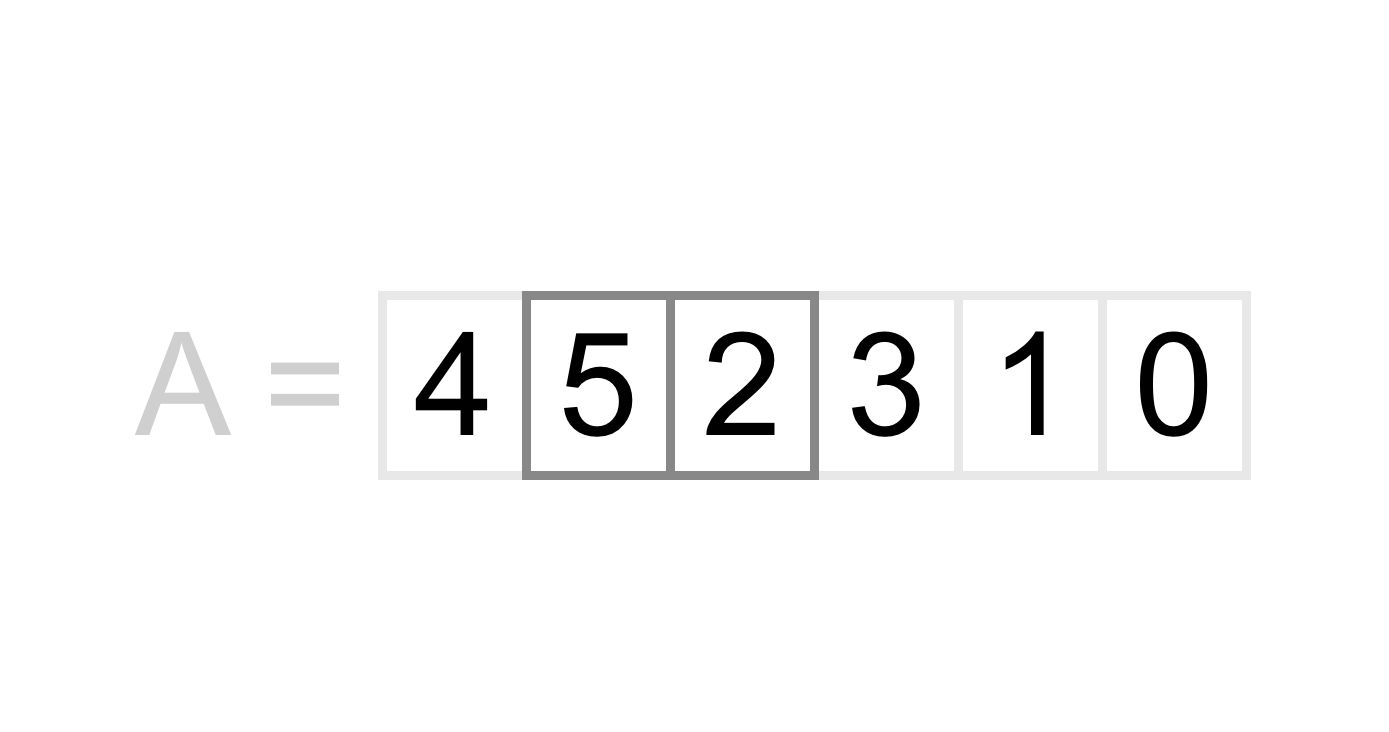
Once again we ask the question “is 5 greater than 2?”, and once again we get the answer yes, so we need to swap these numbers. After swapping we get the following list.

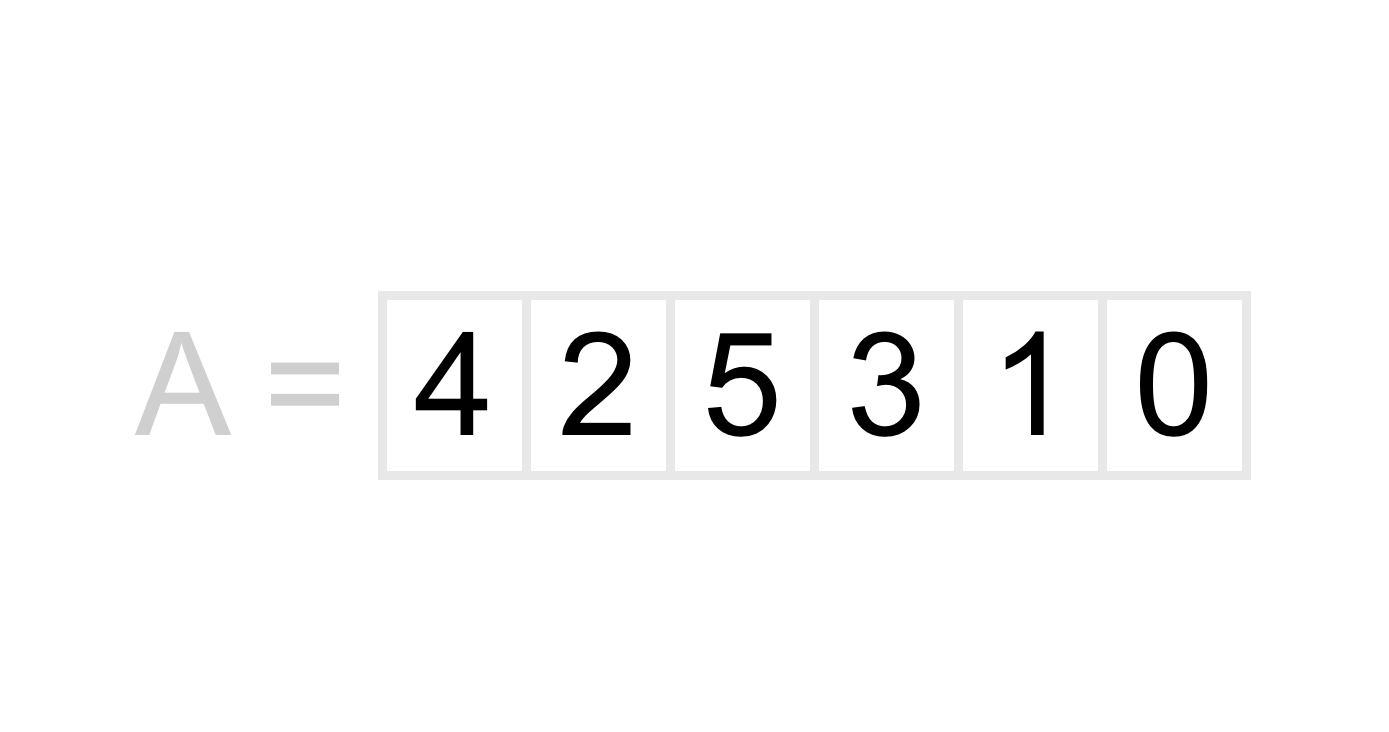
We proceed through the rest of the pairs in the list doing this same comparison until we have reached the end of the list. The next pair we will compare is 5 and 3, which will be swapped. After that we will compare 5 and 1, which again will be swapped. Finally we will compare 5 and 0 which will be swapped as well. After all of these comparisons and swaps we get the following list.

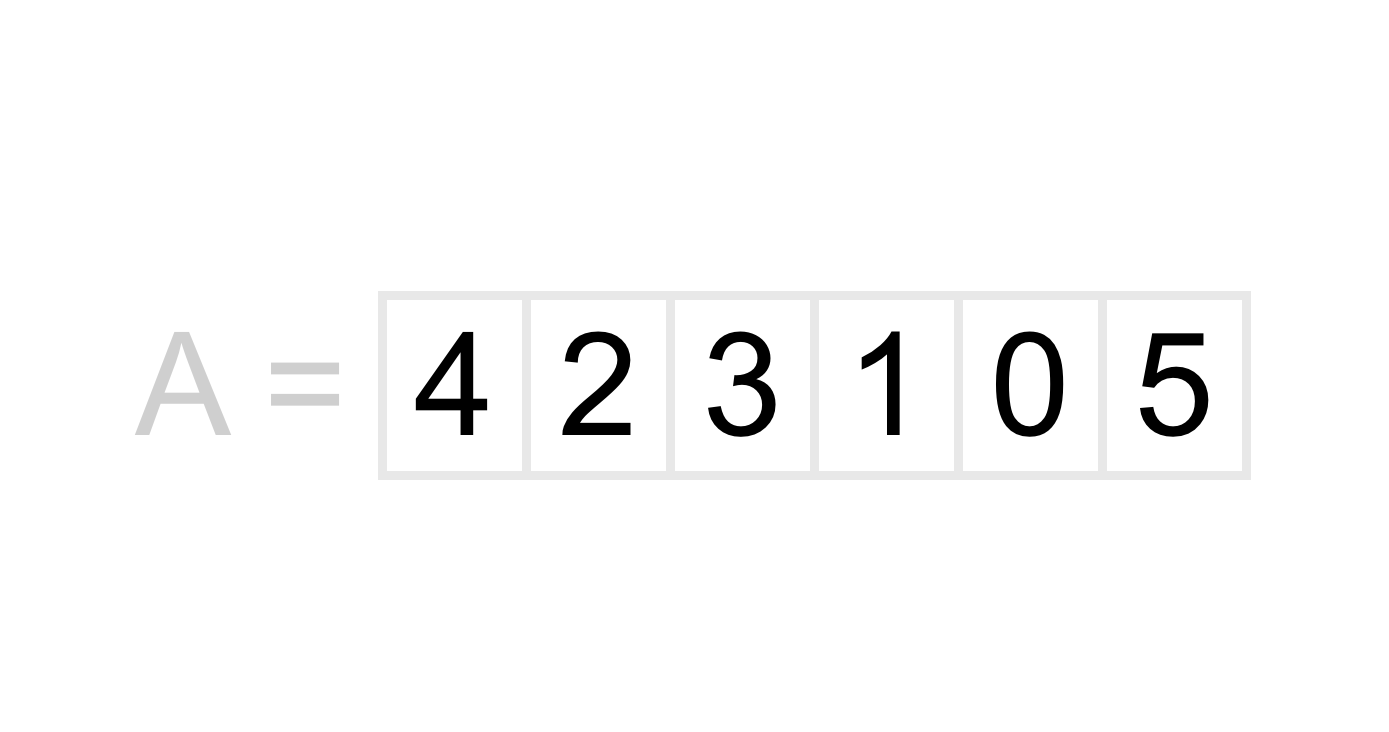
Do you notice anything special about the list after we have made one full pass through it comparing and swapping every consecutive pair where the first number is greater than the second?

If you said the last number in our list is the largest number in the list, you hit the nail on the head!

Rinse and repeat to completely sort the list

Each time we walk through the list we are guaranteed to move the largest number in the list to its final position in the sorted list. The first pass will ensure that the number in the very last position gets moved there. The second pass will ensure that the number in the second to last position gets moved there, and so on.

Try it for yourself. Follow the algorithm described above on paper using the list we got after our first pass.

Start by comparing 4 and 2 and swapping them if 4 is greater than 2 (hint: it is). Then move on to the second consecutive pair and do this for every consecutive pair in the list.

If you did everything correct, you should find that your second pass caused the 4 to get moved to its final position in the sorted list; 4 is in the second to last position in the list!

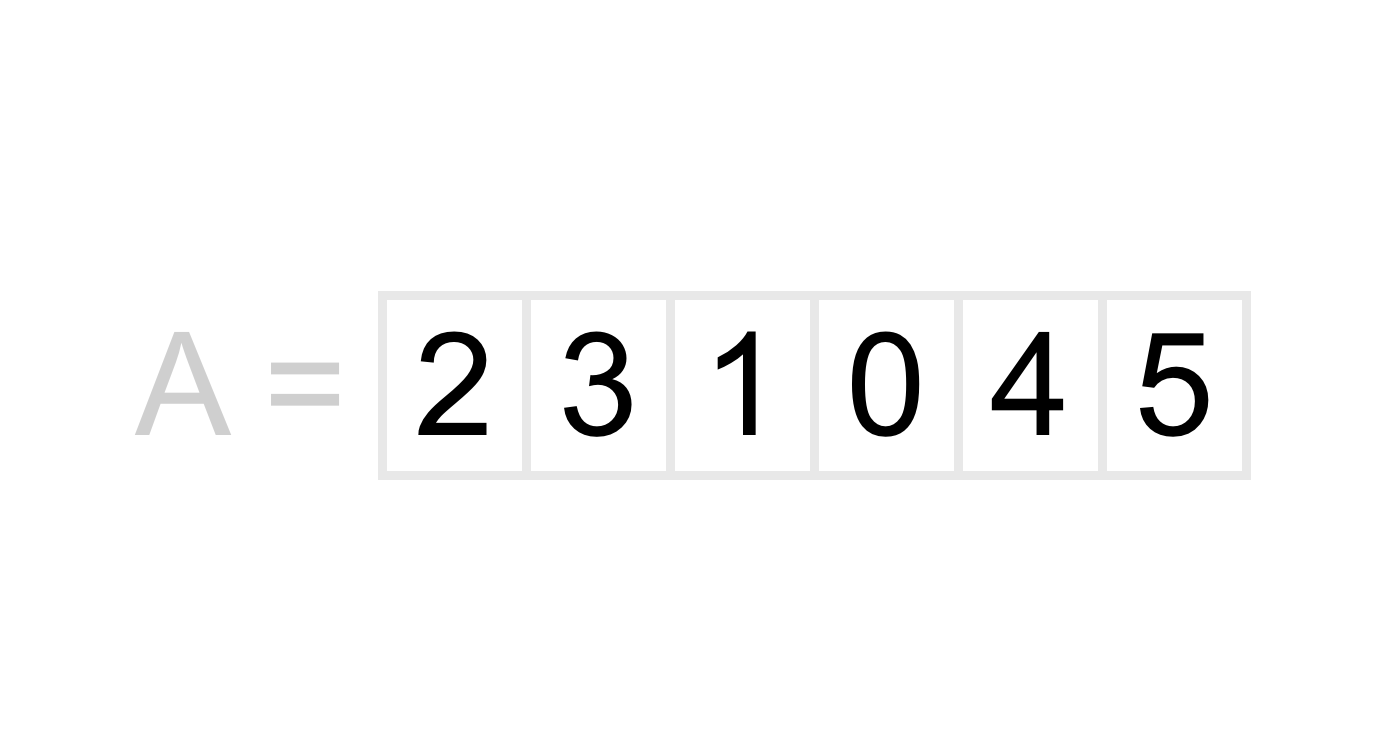
This should start give you a clue about how many times we need to repeat this part of our algorithm. If a list is in complete reverse order (the worst case for bubble sort), we will need to repeat this part of our algorithm one time for every number in the list, or in other words, we will need to repeat this N times if N is the number of items in our list.

Assuming you did the second pass on paper, we should already have 2 of 6 passes complete. Lets look at what the results of each of the last 4 passes would be.

Pass 3 - 2, 1, 0, 3, 4, 5

Pass 4 - 1, 0, 2, 3, 4, 5

Pass 5 - 0, 1, 2, 3, 4, 5

Pass 6 - 0, 1, 2, 3, 4, 5

It turns out that our 6th pass wasn’t even necessary, but we didn’t know that until we made that pass and saw that no numbers were swapped. Later we will discuss how you can take advantage of this to terminate your algorithm early, making it faster in cases where lists are nearly-sorted.

Complexity of bubble sort

While I haven’t written about Big-O notation or how to calculate the complexity of an algorithm, it is worth at least talking about how fast an algorithm is relative to the size of its input.

For the rest of this section you should assume that when I reference N I am referring to the size of the list of numbers we are sorting.

Our bubble sort algorithm can be broken into roughly two pieces. The first is what we have spent most of this article discussing - walking through the list comparing consecutive pairs of numbers. Every time we do a full pass of the list we will look at N - 1 pairs of numbers.

The second part is repeating this walk-through of the list. As we discussed early, in the worst case we would need to repeat this N times, so we end up doing N - 1 comparisons N times, giving us N * (N - 1).

In Big-O we drop the constants, so we get the complexity of O(N*N) or O(N^2). This means that as the size of our list grows, the number of operations we need to sort the list grows exponentially.

Optimizations

There are two major optimizations you can make with bubble sort in your code.

Don’t compare numbers that are in their final position

The first optimization is to stop looking at a number once we know it is in its final position in our list. Remember when we did our first pass of our list above and ended up with the list below?

We know that the 5 is in the correct position after the first pass, so for the second pass and onwards we can skip comparing it to the number before it.

Similarly, after our second pass we know that the second to last number in our list is the second largest number in our list, so we can skip comparing it to numbers before it on the third pass and onwards.

More generally, on the ith pass of our list, we can ignore the last i - 1 items in the list. On the first pass we can ignore the last 0 items. On the second pass we can ignore the last 1 items. On the third pass we can ignore the last 2 items, and so on.

On a completely reversed list this optimization will end up cutting the number of operations required to sort a list in half.

Stop sorting if your list is already sorted

The second optimization is to stop doing new passes where we compare and swap numbers as soon as we realize that our list is already sorted. This leads us to the question, “How do we tell if the list is already sorted?”

Determining if a list is already sorted is actually pretty easy to do with a bubble sort. When we walk through a list comparing numbers, we are basically checking if any numbers in the list are out of order.

If we happen to pass through our entire list and never swap two numbers that means that no numbers were out of order; Or if we inverse that statement, every number was already in order.

When we walk through our list without swapping any numbers we have effectively determined that our list is already sorted, so at that point we can safely terminate our algorithm and return the sorted list of numbers.

While this optimization won’t consistently reduce the number of operations required for your algorithm, it does make your code much more efficient in some cases; Most notably, when dealing with already sorted or nearly sorted lists your algorithm becomes significantly faster.

Up Next…

Now that you have an understanding of how bubble sort works we are going to move on to implementing the algorithm in real code. We will start off a list of integers like in this tutorial, but we will also explore sorting lists of strings and really any other data type.

You can find the next article here - Let's Learn Algorithms: Implementing Bubble Sort.

Have an algorithm you would love to learn about? Check out other articles in the Let's Learn Algorithms series to see if I have already covered it. If I haven’t feel free to get in touch (jon@calhoun.io) and make a request. I am always happy to hear from my readers :)